Durante cinquenta anos, matemáticos do século XIV viviam com uma inquietação: a falta de uma definição da expressão “número real”. Em 1872, alguns matemáticos definiram satisfatoriamente essa expressão. Entretanto, antes de apresentar os números reais, precisamos entender o que são os números racionais e irracionais.
Confira mais a respeito, só aqui no Gestão Educacional!

Números racionais e irracionais
Os números racionais são aqueles que podem ser expressos pela divisão de dois números inteiros. Por exemplo:
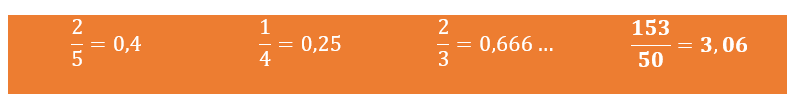
Sabemos que os números racionais não solucionaram muitos dos problemas envolvendo a Geometria e a Aritmética. Em determinadas figuras, os matemáticos gregos da Antiguidade descobriram, em seus estudos, a existência de segmentos cujas medidas não podiam ser representadas por números racionais.
Por exemplo, eles verificaram que √2 era a medida de um desses segmentos.
Os pitagóricos já haviam acusado essa dificuldade com relação à diagonal e ao lado do quadrado. Exemplificando, para um quadrado de lado l =1 e diagonal d, temos:
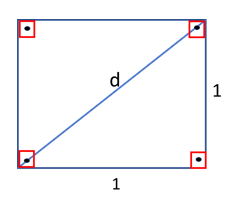
Aplicando o Teorema de Pitágoras no triângulo, obtemos:
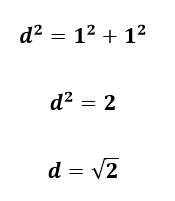
Qual o número cujo quadrado é 2? A resposta é:
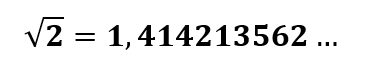
Esse número tem uma infinidade de casas decimais, que não se repetem, portanto, não é uma dízima periódica. Assim, √2 não é um número racional. É um número irracional.
Fica evidente que nem sempre a raiz de um número racional é um número racional. Para que a teoria dos números racionais evoluísse, foi necessário o avanço dos estudos sobre infinitos e geometria analítica.
Os números que não podem ser expressos pela divisão de dois números inteiros, ou seja, na forma p/q, com p e q inteiros e q ≠ 0, são chamados números irracionais.
Além disso, quando esses números são indicados na forma decimal, apresentam infinitas casas decimais e não periódicas. Portanto, podemos resumir com a seguinte afirmação: Número irracional é o número que tem uma representação decimal infinita (não exato) e não periódica.
Exemplos:
- O número π = 3,141592, resultado da divisão da medida do comprimento de uma circunferência pela medida do seu diâmetro;
- O número e= 2,718, conhecido como número de Euler (Leonhard Euler, 1707-1783), ou número neperiano;
- Radicais do tipo √2= 1,4142…; √3= 1,7320…; √5= 2,2360…
Durante algum tempo, a √2 foi o único irracional conhecido. Posteriormente, outros matemáticos mostraram que os números √5, √7, √8, √10 e π eram também irracionais.
Uma curiosidade. O símbolo π é a décima sexta letra do alfabeto grego e é a inicial da palavra grega periferia que significa circunferência. O valor de corresponde à razão entre o comprimento da circunferência C pelo seu diâmetro d, ou seja, π= c/d.
O escritor inglês Willian Jones (1675-1749) foi o primeiro a usar a letra grega π em uma publicação, em 1706. Entretanto, o seu uso definitivo só aconteceu depois que o matemático Leonhard Euler (1707-1783) a adotou, em 1737. O suíço alemão Johan Heinrich Lambert (1728-1777) apresentou, em 1767, a primeira prova mostrando que π é um número irracional.
Reunindo os números racionais com os números irracionais, formamos o conjunto dos números reais, que representamos por .
O que é o conjunto dos números reais?
O conjunto dos números reais é formado pela reunião do conjunto dos números racionais com o conjunto Ir dos números irracionais:
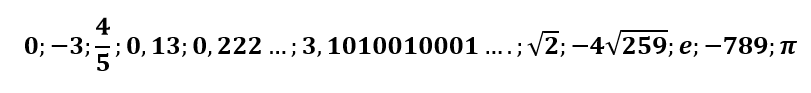
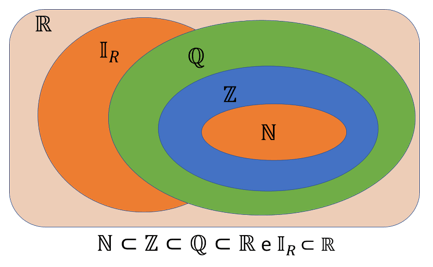
Assim, dizemos que todos os números naturais, inteiros, racionais e irracionais, são números reais. Veja, abaixo, uma possível representação da relação entre os conjuntos numéricos, pelo diagrama:
Além disso, podemos estabelecer uma correspondência um a um entre o conjunto de números reais e o conjunto dos pontos de uma reta. Ou seja, a cada número corresponde um e um só ponto da reta e vice-versa, como mostra a figura, abaixo:
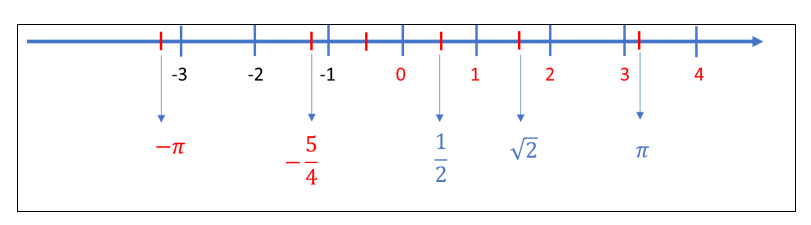
Essa representação geométrica dos números reais é chamada reta numérica real ou, simplesmente, reta real. As noções de números opostos, números inversos e módulo de um número se aplicam aos números reais.
Exemplos

Observe que cada um desses cinco conjuntos contém números racionais e números irracionais.
Exercícios Resolvidos
- a é o inverso de -3/5; b é o oposto de 5/6, e c é o dobro de -√2/3. Disponha a, b e c em ordem crescente.
Resolução:
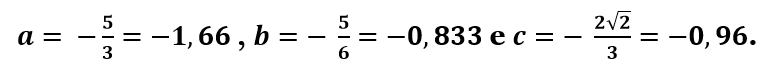
Em ordem crescente, do menor para o maior, teremos a, c e b.
- Determine o valo das expressões:
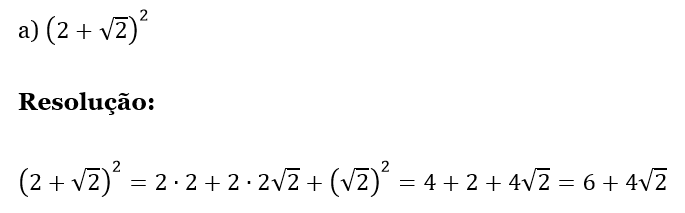
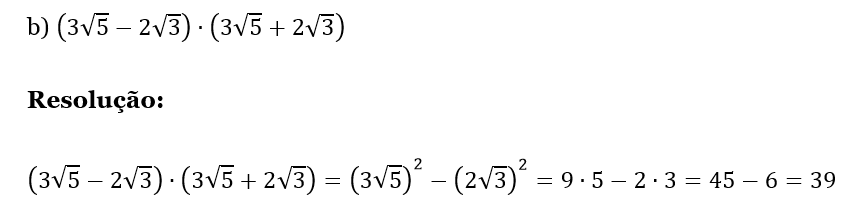

 .
. dos números racionais com o conjunto Ir dos números irracionais:
dos números racionais com o conjunto Ir dos números irracionais: