Ondulatória é a área da física que estuda ondas. Nos meios elásticos, as oscilações se propagam, dando origem às ondas. Por exemplo, ao cair uma pedra na superfície de um lago, essa pedra desloca certo volume de água, tanto lateralmente quanto verticalmente. Ao descer, a porção de água que se projeta acima do nível normal chega à posição de equilíbrio, mas desloca lateralmente e verticalmente uma nova porção de água ao seu redor. Assim, a oscilação mecânica vai se propagando pela superfície do lago.
Propagação ondulatória
Considere uma corda esticada e bem longa. Uma perturbação provocada em uma das extremidades da corda chega até a outra extremidade. Se colocarmos uma fita amarrada na corda, essa fita irá subir e descer com a passagem da oscilação, porém não será transportada.
Essa perturbação que se propaga ao longo da corda recebe o nome de onda. Uma característica fundamental da propagação da onda é:
- “As ondas transportam energia sem transporte de matéria”.
As propagações ondulatórias são classificadas com base nos seguintes critérios: direção da vibração, natureza da vibração e graus de liberdade para a propagação das ondas.
Direção da vibração
Dizemos que ocorre propagação transversal quando a direção da vibração é perpendicular à direção de propagação da onda. Já a propagação longitudinal ocorre quando a direção da vibração é a mesma na qual se efetua a propagação da onda.
O som é um exemplo de propagação longitudinal.

Nas propagações mistas, ambas as situações anteriores ocorrem simultaneamente. É o caso de perturbações que se propagam na superfície de líquidos.
Natureza da vibração
Nas propagações mecânicas ocorre o transporte de vibrações mecânicas. As ondas mecânicas precisam de um meio material para sua propagação, por isso, o som não se propaga no vácuo.
Alguns exemplos de propagações mecânicas são ondas em cordas, molas, superfície e interior de líquidos e gases, etc.
As propagações eletromagnéticas correspondem a variações nos campos elétrico e magnético, originadas por cargas elétricas oscilantes. É o caso das ondas de rádio, microondas, luz visível, raio X, etc. Essas ondas não necessitam, obrigatoriamente de um meio material para sua propagação, podendo até se propagar no vácuo.
Graus de liberdade para a propagação das ondas
Nas propagações unidimensionais, as ondas se deslocam sobre uma linha (as ondas em uma corda, por exemplo).
Nas propagações bidimensionais, as ondas são produzidas em uma superfície, por exemplo, as ondas nas superfícies de líquidos.
Nas propagações tridimensionais, as ondas se propagam em todas as direções, como a propagação do som no ar.
Velocidade dos pulsos
Chama-se pulso a onda que corresponde a uma perturbação simples.
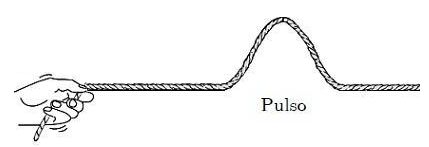
A velocidade de propagação de um pulso é dada por: (sendo v a velocidade, T a tração e μ a densidade linear, definida por μ = m/L – massa/comprimento da corda).
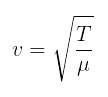
Ondas periódicas
Uma sucessão de pulsos iguais produz uma onda periódica. Nas ondas periódicas, destacamos:
- Elongação (y): valor algébrico da ordenada do ponto oscilante da corda;
- Amplitude da onda (A): maior valor da elongação, está relacionado à energia transportada pela onda;
- Frequência (f): número de oscilações executadas por qualquer ponto da corda, por unidade de tempo;
- Período (T): intervalo de tempo de uma oscilação completa de qualquer ponto da corda;
- Pontos C1 e C2 são cristas, e os pontos V1, V2 e V3 são vales;
- Dois pontos estão em concordância de fase quando têm sempre o mesmo sentido do movimento;
- Dois pontos estão em oposição de fase quando têm sempre sentidos de movimentos opostos;
- Comprimento da onda (λ) é a menor distância entre dois pontos que vibram em concordância de fase. Isto é, é a distância entre duas cristas ou dois vales consecutivos.
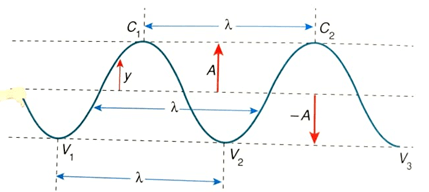
As distâncias entre os pontos C1 e C2 é o comprimento da onda λ. Essa distância é percorrida pela onda no período T. Assim, temos que a frequência f e a velocidade v de propagação da onda são dadas por:
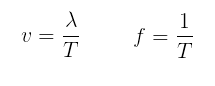
Temos também a equação fundamental da ondulatória, dada por:
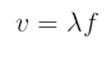
Equação da onda
Vamos considerar que na extremidade esquerda de uma corda extensa esteja acoplada uma fonte de oscilações harmônicas, cuja elongação em função do tempo seja dada por:
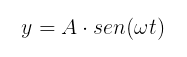
Um ponto qualquer da corda, cuja abscissa seja x, irá oscilar da mesma forma, mas com um atraso não-nulo em relação à origem, devido ao tempo de propagação da onda.
A função horária da elongação desse ponto também pode ser dada por: