O Princípio de Huygens afirma que cada ponto de uma frente de onda se comporta como uma nova fonte de ondas elementares e progressivas. A linha ou a superfície que tangencia todas as ondas elementares produzidas correspondem à frente de onda em um instante posterior.
Assim como Newton formulou os princípios da Mecânica, coube a Christian Huygens sistematizar as leis de propagação da ondulatória.
Na Física Moderna, a Mecânica das Partículas e a Mecânica Ondulatória estão sempre presentes. Alguns fenômenos só são entendidos e explicados pela ondulatória; outros, exclusivamente pela Mecânica das Partículas; e há ainda outros, comumente vistos em Física Nuclear, em que tanto a Mecânica como a ondulatória contribuem para o seu entendimento.
Ondas periódicas e dimensões da onda
Chama-se pulso a onda que corresponde a uma perturbação simples.
Uma sucessão de pulsos iguais produz uma onda periódica.
Nas propagações unidimensionais, as ondas se deslocam sobre uma linha (as ondas em uma corda, por exemplo).
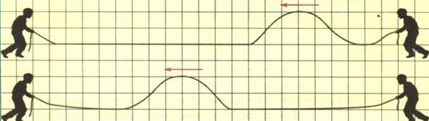
Nas propagações bidimensionais, as ondas são produzidas em uma superfície, como as ondas nas superfícies de líquidos.
Nas propagações tridimensionais, as ondas se propagam em todas as direções, por exemplo a propagação do som no ar.
Frente da onda
Em meios bi ou tridimensionais, as perturbações oriundas de uma fonte se propagam em todas as direções.
Para entender o princípio de Huygens, devemos inicialmente compreender o que significa frente da onda.
Suponha que você tirasse uma fotografia das ondulações que se espalham em um lago. Se você marcasse o local das cristas nas fotos, sua imagem seria parecida com a figura abaixo:
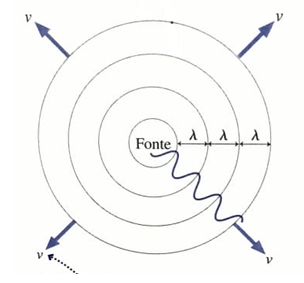
As linhas que localizam as cristas são chamadas de frentes de onda e estão espaçadas precisamente em um comprimento de onda (λ).
O diagrama acima mostra apenas um único instante de tempo, mas você pode imaginar um filme no qual visse as frentes de onda se movendo para longe da fonte com velocidade v (como mostra as setas em azul). Uma onda como essa é denominada onda bidimensional.
Ou seja, uma frente de onda corresponde a uma linha ou a uma superfície, formada por pontos da onda em um determinado instante que estejam em concordância de fase e que separem a região perturbada da região não perturbada pela propagação ondulatória.
Lembrando que:
- Elongação:valor algébrico da ordenada (valor de y do ponto) oscilante da corda;
- Dois pontos estão em concordância de fase quando têm o mesmo sentido de movimento. Ou seja, esses pontos apresentam a mesma elongação e se movem no mesmo sentido.
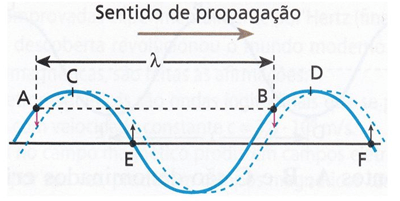
No exemplo acima, os pontos em concordância de fase são: A e D, C e B, E e F.
No caso de uma fonte puntiforme, emitindo num meio bidimensional, as linhas de onda são circunferências concêntricas, tendo por centro a fonte emissora. Tais ondas são ditas ondas circulares.
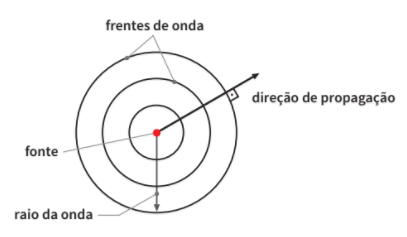
Caso a fonte puntiforme emita num meio tridimensional, as superfícies de onda serão esferas concêntricas, sendo a fonte o centro comum. Tais ondas são denominadas ondas esféricas.
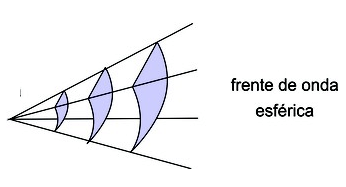
Embora as frentes de onda sejam círculos, você dificilmente notaria a curvatura se observasse uma pequena secção da frente da onda a uma distância muito grande da fonte. As frentes de onda pareceriam linhas paralelas, espaçadas por um comprimento de onda que se propaga com velocidade v.
Um bom exemplo é o de uma onda oceânica a centenas ou milhares de quilômetros da costa. Quando as ondas à praia onde você está se bronzeando, as cristas parecem linhas retas.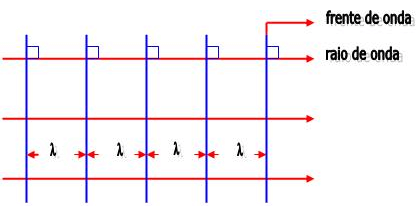
Princípio de Huygens-Fresnel
Este princípio diz que cada ponto de um meio atingido por uma perturbação periódica torna-se, por sua vez, uma nova fonte de perturbação periódica. O princípio pode ser enunciado da seguinte maneira:
“Se uma perturbação periódica se propaga num meio qualquer, e se S é a frente de onda da perturbação, correspondente a um instante t qualquer, cada ponto de S torna-se um foco emissor secundário de ondas elementares, independentes entre si e de frequências iguais à da fonte. A nova frequência de onda S’ correspondente ao instante t + Δt é a envolvente de todas as frentes de ondas elementares emitidas pelos pontos de S e desenvolvidas durante o intervalo de tempo Δt”.
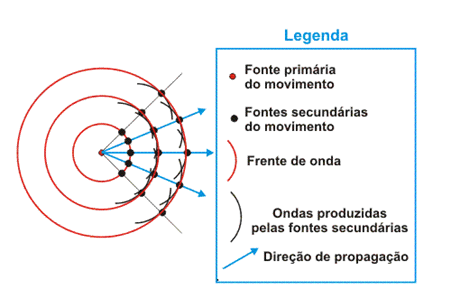Quando observamos a uma distância grande da fonte, como dito anteriormente, temos:
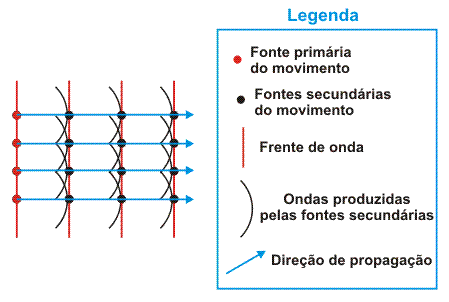
Portanto, teremos ondas circulares no caso de um meio bidimensional e ondas esféricas no caso de um meio tridimensional.
