O matemático Leonardo de Pisa, mais conhecido como Fibonacci, viveu na Idade Média e contribuiu com diversas pesquisas para o desenvolvimento da matemática, entre elas a constatação da sequência numérica presente em vários fenômenos naturais. Fibonacci registrou uma sequência que levaria o seu nome: ela começa por 1 e cada número seguinte é a soma dos dois números anteriores.
As sequências matemáticas podem ser escritas por uma lei de formação, como é o caso das progressões aritméticas e geométricas que veremos a seguir aqui, no Gestão Educacional.
Progressão aritmética: o que é?
Progressão aritmética é toda sequência de números na qual a diferença entre cada termo (a partir do segundo) e o termo anterior é constante.
Essa diferença é chamada de razão da progressão e é representada pela letra r.
Para entendermos melhor, vamos analisar alguns exemplos.
- A sequência (2, 7, 12, 17, …) é uma progressão aritmética infinita, de razão 5.
- O primeiro termo é chamado de a1 = 2.
- A razão r é dada por: r = 7- 2 = 5.
- A sequência (4, 4, 4) é uma PA de 3 termos, em que o primeiro é a1 = 4 e a razão é r = 0
- A sequência (1, -1, 1, -1, 1, -1, …) não é uma progressão aritmética porque as diferenças entre termos sucessivos são alternadamente –2 e 2.
- A sequência (10, 4, -2, -8, …) é uma PA com r = -6
De modo geral, uma sequência é uma PA quando:
- an = an-1 + r;
- an – an-1 =
Termo geral de uma PA
Em uma progressão aritmética (a1, a2, a3, …, an, …) de razão r, encontramos o termo de ordem n, denominado termo geral da PA, da seguinte maneira: an = a1 + (n-1).r – sendo:
- a1 = 1º termo;
- an = termo geral;
- n= número de termos (até an);
- r = razão da PA.
Também podemos encontrar o termo geral de outra forma: an = ak + (n – k).r – sendo k é o número de termos até ak, e ak um dos termos dessa PA.
Soma dos termos de uma PA finita
Considerando a PA finita de razão r (a1, a2, a3, …, an-2, an-1, an), a soma dos seus n termos pode ser escrita por: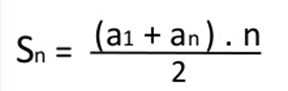
Em que:
- a1 = primeiro termo;
- an = enésimo termo;
- n= número de termos (até an);
- Sn é a soma dos n termos.
Propriedades da PA
- A partir do segundo termo, qualquer termo da PA é sempre igual à média aritmética entre os termos anterior e posterior dele;
- Em uma PA finita, a soma de dois termos equidistantes é igual à soma de dois termos extremos;
- Em uma PA com número ímpar de termos, o termo médio é igual à média aritmética dos termos extremos.
Progressão geométrica (PG)
Progressão geométrica (PG) é toda sequência de dois números não nulos na qual, a partir do segundo termo, o quociente da divisão de um termo pelo termo anterior é constante.
Esse quociente constante é chamado de razão (q) da progressão.
A diferença entre PA e PG se dá pelo modo como o próximo termo é formado:
- Em PA, somamos a razão r com um termo para obter o próximo;
- Em PG, multiplicamos a razão q com um termo para obter o próximo.
Exemplo:
A sequência (1, 3, 9, 27, …) é uma PG infinita, na qual a1 = 1 e q = 3, pois:
- a1 = 1;
- a2 = 1 . 3 = 3;
- a3 = 3 . 3 = 9;
- a4 = 9 . 3 = 27.
E assim por diante.
Fórmula do termo geral de uma PG
O termo de ordem n, denominado termo geral de uma PG, é dado por: an = a1 . qn-1 – sendo:
- an = termo geral;
- n = número de termos, até an;
- a1 = 1º termo;
- q = razão.
Esse termo também pode ser dado por: an = ak . qn-k – sendo k o número de termos até ak, e ak um dos termos dessa PA.
Soma dos n primeiros termos de uma PG finita
A soma dos n primeiros termos de uma progressão geométrica finita de razão q ≠ 1 é dada por: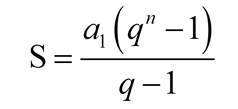
Propriedades da PG
- O quadrado de qualquer termo de uma PG, a partir do segundo, é sempre igual ao produto do termo que o antecede pelo termo que o sucede;
- Em uma PG finita, o produto de dois termos equidistantes é igual ao produto dos termos extremos;
- Se a PG tiver número ímpar de termos, o quadrado do termo médio é igual ao produto dos termos anteriores.
Exercício resolvido
1) Determine o valor de x de modo que os números x+1, x+4 e x+10 formem, nessa ordem, uma PG.
RESPOSTA:
Como são três termos consecutivos, temos:
(x+4)² = (x+1)(x+10)
X² + 8x + 16 = x² + 11x + 10
3x = 6
X = 2
Logo, o valor procurando é x = 2 e os números são 3, 6, 12.
