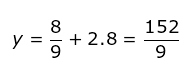Identidades trigonométricas surgiram na Grécia Antiga e eram expressas na forma equivalente de cordas. Porém, obras feitas por matemáticos hindus, que vão dos séculos V a XII, estabeleceram as fórmulas que conhecemos hoje como relações trigonométricas.
As relações surgem umas a partir das outras por raciocínio dedutivo, sendo que a principal relação trigonométrica teve origem com o Teorema de Pitágoras.
A seguir, veja quais são as principais relações trigonométricas que você deve estudar e como utilizá-las, só aqui no Gestão Educacional!
O que são as relações trigonométricas?
Além de seno, cosseno e tangente, existem outras três funções trigonométricas importantes por seu valor histórico: secante, cossecante e cotangente.
As relações entre os valores das funções trigonométricas de um mesmo arco são denominadas relações trigonométricas.
Vamos, abaixo, conhecer as relações trigonométricas fundamentais.
Relações fundamentais
Observe o círculo trigonométrico de raio igual a 1: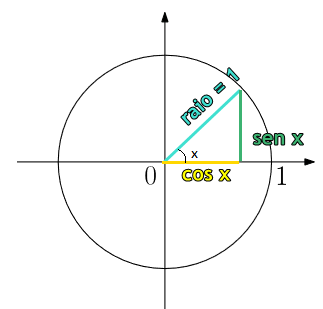
Ao criar um triângulo retângulo, em seu centro, temos que a hipotenusa é exatamente o raio do círculo e os dois catetos são os valores de seno e cosseno do ângulo x.
[CLIQUE AQUI PARA SABER MAIS SOBRE A ÁREA DO CÍRCULO]
Pelo Teorema de Pitágoras, temos que para todo x real, x ∈ [0, 2π], vale: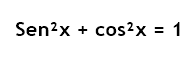
Essa é umas das relações fundamentais.
Ainda no círculo trigonométrico, vamos traçar uma reta tangente a ele no ponto S, que é a reta em vermelho na figura abaixo: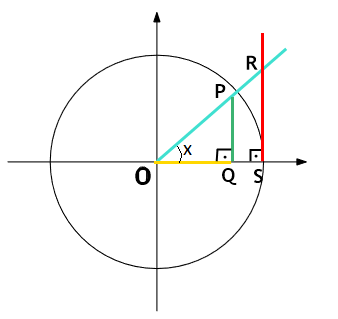
Os triângulos ΔOPQ e ΔORS possuem dois ângulos correspondentes congruentes. Portanto, são triângulos semelhantes.
Por semelhança, podemos dizer que: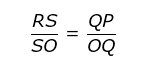
Sendo OQ = cos x e QP = sen x, temos:
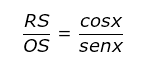Sendo RS = tg x e OS = 1 (pois OS é exatamente o raio do círculo), temos:
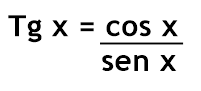Essa é a segunda relação fundamental.
Além disso, existem outras relações fundamentais, que são as relações a seguir: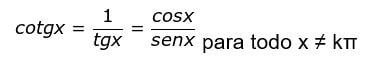
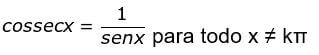Agora, a partir dessas relações fundamentais, iremos encontrar outras. Veja, a seguir, como achar outras relações a partir dessas que já aprendemos.
Relações decorrentes das fundamentais
Para todo x real, x ∈ [0, 2π] e x ∉ [0, π/2, π, 3π/2, 2π], vale as cinco relações:
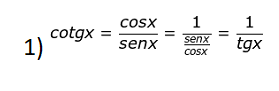
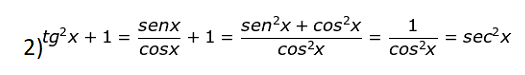
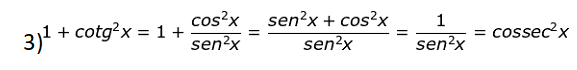
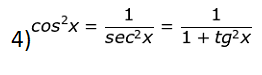
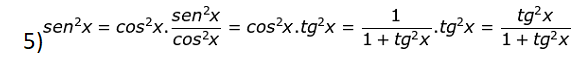Resumindo, podemos criar o seguinte esquema: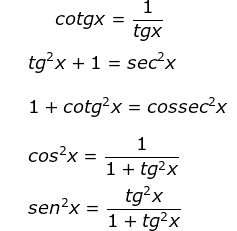
Exercício resolvido
1) Sabendo que sec x = 3, calcule o valor da expressão y = sen²x + 2.tg²x
SOLUÇÃO: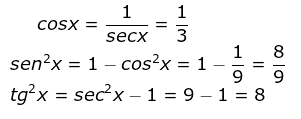
Então:
