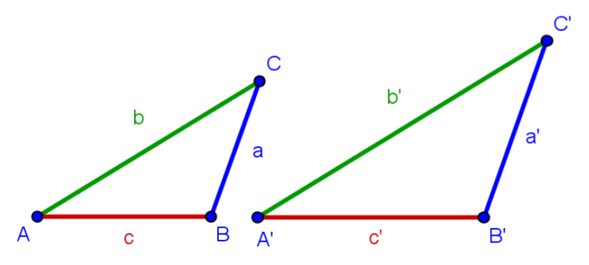
Figuras semelhantes são aquelas que têm a mesma forma, mas não necessariamente o mesmo tamanho. Figuras congruentes também são semelhantes.
Quando projetamos um slide em uma tela, por exemplo, a imagem projetada geralmente tem o tamanho diferente da original, mas conserva a mesma forma. Dizemos que a figura que aparece na tela é semelhante à original.
As fotocopiadoras também reproduzem cópias em tamanho ampliado ou reduzido, mas mantendo a forma do original. Para obter na fotocopiadora uma ampliação de, por exemplo, 50%, devemos digitar 150%, pois a ampliação deverá ser igual à original (100%) aumentado de 50%. Querendo uma redução de 25%, digitamos 75%, que corresponde à original (100%), diminuindo 25%.
Ampliando ou reduzindo imagens em uma fotocopiadora, estamos obtendo figuras semelhantes às originais.
Polígonos semelhantes
Em papel quadriculado, é fácil obter ou reduzir figuras. Abaixo, ampliamos um polígono em 400%.
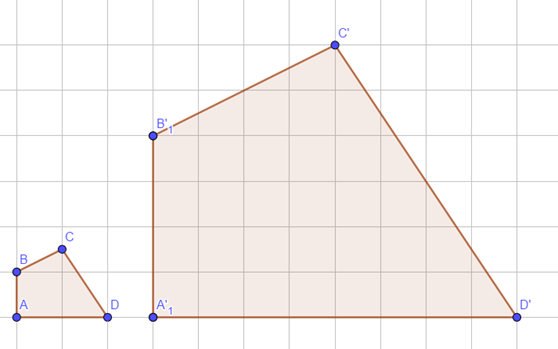
Os ângulos A e A’, B e B’, C e C’, D e D’ são chamados ângulos correspondentes. Observe que eles são congruentes (têm a mesma medida).
Os pares de lados AB e A’B’, BC e B’C’, CD e C’D’, AD e A’D’ são chamados lados correspondentes. Eles são proporcionais:
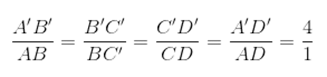
Concluímos, assim, que o polígono ABCD é semelhante ao polígono A’B’C’D, e indicamos essa semelhança da seguinte forma: ABCD ~ A’B’C’D.
Nesse caso, dizemos que a razão de semelhança K entre o polígono ampliado (A’B’C’D) e o polígono original (ABCD) é 4. Isto é, qualquer lado do polígono A’B’C’D tem por medida o quadruplo da medida do seguimento correspondente em ABCD. Portanto, a razão de semelhança dessa ampliação é k = 4.
Com isso, podemos afirmar que dois polígonos são semelhantes quando:
- Os lados correspondentes são proporcionais;
- Os ângulos correspondentes são congruentes.
Área e perímetro de figuras semelhantes.
A razão entre o perímetro de duas figuras semelhantes é a razão de semelhança k. Enquanto isso, a razão entre a área de duas figuras semelhantes é k².
Por exemplo, calculando a área das figuras abaixo, temos que:
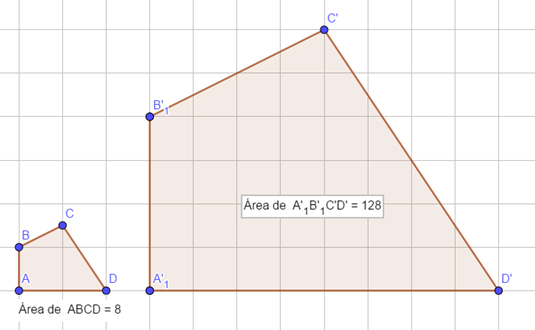
AABCD = 8 e AA’B’C’D’ = 128. A razão entre as duas áreas será igual ao quadrado da razão de semelhança:
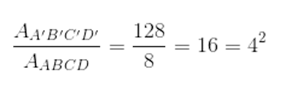
Encontramos exatamente a razão de semelhança k = 4. Agora, observe as figuras abaixo:
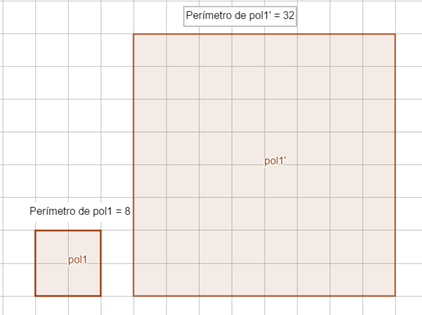
O segundo polígono é uma ampliação do primeiro. Para encontrar a razão de semelhança dessa ampliação, vamos calcular a razão de seus perímetros:
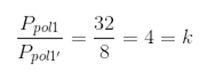
Semelhança aplicada a triângulos
Dois triângulos são semelhantes quando a medida de seus ângulos correspondentes é igual. Essa é uma característica que pode ser aplicada apenas aos triângulos, pois para os outros polígonos serem semelhantes, além dos ângulos correspondentes congruentes, a medida dos lados também deve ser conferida, e é preciso verificar se existe proporcionalidade entre eles.
Na figura abaixo, os triângulos ABC e DEF são semelhantes. Os ângulos pintados da mesma cor são ângulos correspondentes e também são congruentes.
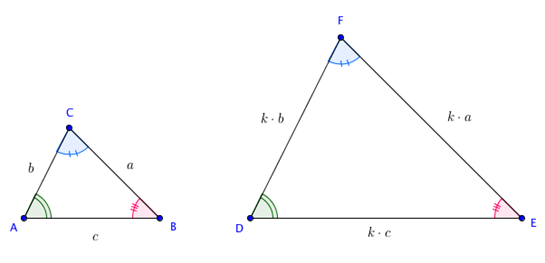
Além disso, os lados correspondentes, consequentemente, são proporcionais.
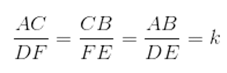
Nesse caso, são proporcionais pois se relacionam pela razão de semelhança k.
As medidas dos lados do triângulo ABC são a, b e c. Para o triângulo DEF ser semelhante a ABC, devemos multiplicar as medidas a, b e c pela constante k. Portanto, as medidas dos lados do triângulo DEF são k.a, k.b e k.c.
Como os dois triângulos são semelhantes, podemos afirmar que:
- A e D são ângulos congruentes (ângulos com a mesma medida);
- B e E são ângulos congruentes;
- C e F são ângulos congruentes;
- A razão entre as alturas correspondentes é k;
- A razão entre duas medianas correspondentes é k;
- A razão entre duas bissetrizes correspondentes é k;
- Os lados correspondentes são proporcionais, ou seja, existe um número real positivo k, tal que:
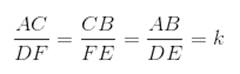
Teorema fundamental da semelhança
“Toda reta paralela a um dos lados de um triângulo e que cruza os outros dois lados em dois pontos distintos determina um triângulo semelhante ao primeiro”.
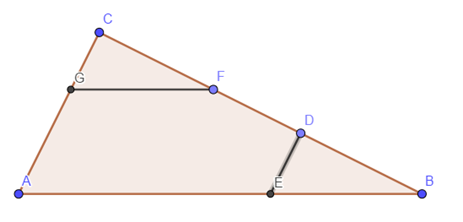
No triângulo ABC, temos:
- DE // CA;
- AB // GF.
Com isso, de acordo com o Teorema Fundamental da semelhança, os triângulos CGF, DEB e ABC são semelhantes.
Casos de semelhança de triângulos
1° CASO: A. A. (ÂNGULO, ÂNGULO)
Se dois triângulos têm dois ângulos congruentes, então esses triângulos são semelhantes:
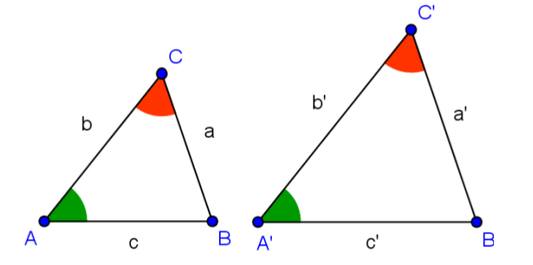
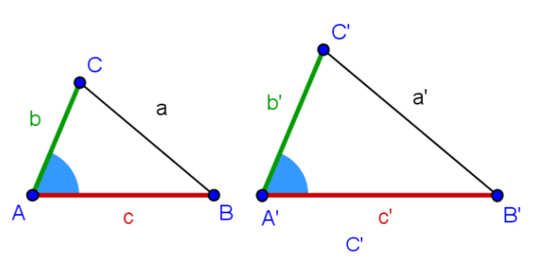
2° CASO: L.A.L (LADO, ÂNGULO, LADO)
Se dois triângulos têm dois lados correspondentes proporcionais e os ângulos compreendidos por esses lados são congruentes, então esses triângulos são semelhantes:
3° CASO: L.L.L. (LADO, LADO, LADO)
Se dois triângulos têm os três lados correspondentes proporcionais, então esses triângulos são semelhantes.