Semelhantes de triângulos – O que são? Teorema fundamental, Casos e Exemplos
Dois triângulos são semelhantes quando a medida dos seus ângulos correspondentes é igual. Essa é uma característica que pode ser aplicada apenas aos triângulos, pois, para os outros polígonos serem semelhantes, além dos ângulos correspondentes congruentes, a medida dos lados também deve ser conferida, e é preciso, também, verificar se existe proporcionalidade entre elas.
Essa propriedade dos triângulos é usada para resolvermos diversos problemas, e há muitos séculos existem instrumentos para medir ângulos. Na astronomia e na navegação, por exemplo, é essencial saber usar esses instrumentos, bem como conhecer semelhança de triângulos. Topógrafos usam teodolitos para medir ângulos e distâncias e, junto com conhecimentos matemáticos, como os do texto a seguir, elaborar plantas e mapas.
Figuras semelhantes
Geralmente, quando dizemos que duas coisas são semelhantes, estamos falando que elas são parecidas. Na matemática, para duas figuras serem semelhantes, elas precisam ter ângulos correspondentes semelhantes (iguais) e lados com medidas proporcionais.
A semelhança entre figuras ocorre a partir de uma ampliação ou redução perfeita. Por exemplo: dois triângulos retângulos são sempre semelhantes. Seus ângulos são sempre iguais (60º) e seus lados aumentam ou diminuem todos proporcionalmente.
Dois cubos e círculos também são sempre semelhantes. Porém, nem sempre dois triângulos são semelhantes. Precisamos então estabelecer alguns critérios que precisam ser confirmados para dois triângulos serem iguais.
Semelhança de triângulos: o que é?
Dois polígonos são semelhantes quando satisfazem duas condições:
- As medidas dos lados que se correspondem são proporcionais;
- As medidas dos ângulos que se correspondem são iguais.
Porém, para dois triângulos serem semelhantes, basta que os seus ângulos respectivos sejam iguais. Mas lembre-se: essa propriedade só é válida para triângulos.
Na figura abaixo, os triângulos ABC e DEF são semelhantes. Os ângulos pintados da mesma cor são iguais.
Além disso, existe uma constante k chamada de razão de semelhança. Essa constante é o número usado para multiplicar a medida de todos os lados do triângulo ABC e assim obter a medida dos lados do triângulo DEF.
Veja que as medidas dos lados do triângulo ABC são a, b e c. Para o triângulo DEF ser semelhante a ABC, devemos multiplicar as medidas a, b, c pela constante k.
Portanto, analisando a figura abaixo, você verá que as medidas dos lados do triângulo DEF são k.a, k.b e k.c. 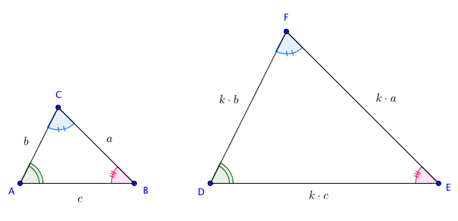 Caso você não conheça essa constante, mas saiba a medida de dois lados correspondentes, podemos estabelecer a seguinte relação para encontrá-la:
Caso você não conheça essa constante, mas saiba a medida de dois lados correspondentes, podemos estabelecer a seguinte relação para encontrá-la: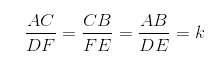 RESUMINDO:
RESUMINDO:
Como os dois triângulos são semelhantes, podemos afirmar que:
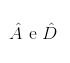 são ângulos congruentes (ângulos com a mesma medida);
são ângulos congruentes (ângulos com a mesma medida);
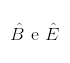
são ângulos congruentes;
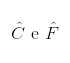
são ângulos congruentes;
Os lados correspondentes são proporcionais, ou seja, existe um número real positivo k, tal que: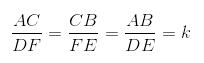
Teorema fundamental da proporcionalidade
Se uma reta paralela a um dos lados do triângulo corta os outros dois lados de um em dois pontos diferentes, os dois triângulos formados serão semelhantes.
Na figura abaixo, os triângulos ABC e ADE são semelhantes
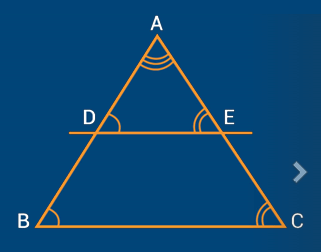
Ou seja, basta a reta DE ser paralela à BC que podemos concluir que os triângulos ABC e ADE são semelhantes.
Outro caso especial desse teorema é o seguinte: se duas retas paralelas são cortadas por duas retas transversais, dois triângulos semelhantes são formados. Observe a figura abaixo: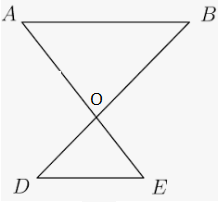 O triângulo ABO é semelhante ao triângulo ODE.
O triângulo ABO é semelhante ao triângulo ODE.
Casos de semelhança de triângulo
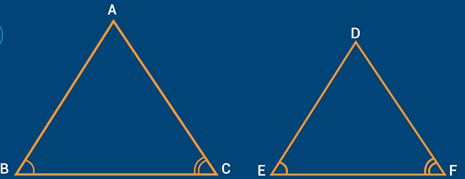
Caso A.A. (ângulo – ângulo)
- Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
Caso L.A.L. (lado – ângulo – lado)
Para esse caso ocorrer, precisamos que:
1) Dois lados de um triângulo são proporcionais a dois lados de outro triângulo;
2) Os ângulos internos formados por esses lados são congruentes.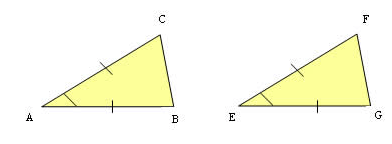
Caso L.L.L (lado – lado – lado)
Se os três lados de um triângulo forem proporcionais com os lados correspondentes de outro triangulo, os dois são semelhantes.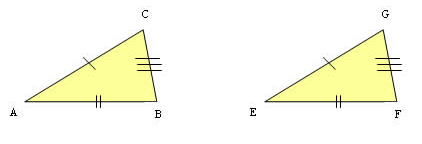
Caso L.A.A (lado – ângulo – ângulo)
Para termos esse caso, os triângulos devem ter os ângulos opostos e adjacentes a um lado com a mesma medida. Além disso, esse lado desse ser proporcional ao lado do outro triângulo.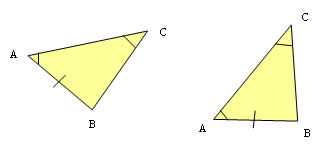
Caso A.L.A (ângulo – lado – ângulo)
Dois triângulos são semelhantes se existir um lado proporcional ao lado do outro triângulo. Além disso, os ângulos que tocam os extremos desse lado devem ser iguais.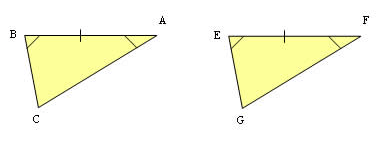





Deixe seu comentário