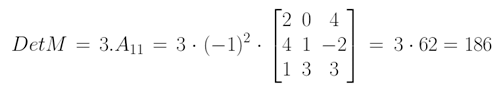O Teorema de Laplace é utilizado para calcular o determinante de uma matriz quadrada de ordem n ≥ 2. Esse método consiste em escolher uma das filas (linha ou coluna) da matriz e somar os produtos dos elementos dessa fila pelos seus respectivos cofatores. O teorema é bastante utilizado quando precisamos calcular o determinante de uma matriz de ordem maior ou igual a três.
Em meados do século XVII, eram estudados os processos para a resolução de sistemas lineares de equações. Nesse período, iniciaram os estudos sobre a teoria de determinantes que conhecemos hoje. Atualmente, utilizamos determinantes para sintetizar certas expressões matemáticas complicadas.
Matriz quadrada e elementos de uma matriz
Uma matriz é quadrada quando possui o mesmo número de linhas e colunas, ou seja, a matriz Am,n é quadrada quando m = n.
Matrizes possuem elementos que podem ser indicados pela linha e coluna em que estão, como mostra a figura abaixo: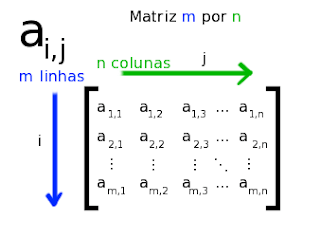 Para calcular o determinante de uma matriz pelo Teorema de Laplace, precisamos conhecer os conceitos de menor complementar e cofator.
Para calcular o determinante de uma matriz pelo Teorema de Laplace, precisamos conhecer os conceitos de menor complementar e cofator.
Menor complementar do elemento
Considerando uma matriz M de ordem n ≥ 2, seja aij um elemento de M, vamos definir o menor complementar do elemento aij e indicaremos ele por Dij.
Dij será o determinante da matriz que se obtém suprimindo a linha i e a coluna j da matriz M. Observe o exemplo abaixo: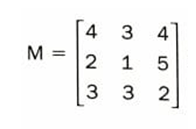 Para calcular o menor complementar do elemento a11 = 4, iremos suprimir a linha 1 e a coluna 1. Depois, calcularemos o determinante da matriz que se obtém após fazermos isso.
Para calcular o menor complementar do elemento a11 = 4, iremos suprimir a linha 1 e a coluna 1. Depois, calcularemos o determinante da matriz que se obtém após fazermos isso.
Cofator de um elemento
Um elemento aij de uma matriz M possui um cofator Aij, indicado por: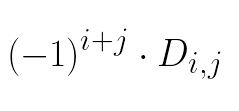 Ou seja, para encontrar o cofator Aij de um elemento, basta multiplicar Dij (menor complementar) por (-1)i+j, sendo i o número da linha e j o número da coluna do elemento.
Ou seja, para encontrar o cofator Aij de um elemento, basta multiplicar Dij (menor complementar) por (-1)i+j, sendo i o número da linha e j o número da coluna do elemento.
Observe os exemplos abaixo: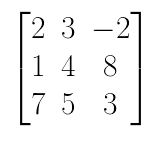 Vamos calcular os cofatores dos elementos da linha 1: A11, A12 e A13.
Vamos calcular os cofatores dos elementos da linha 1: A11, A12 e A13.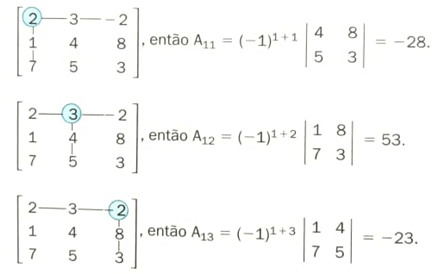
O que é o Teorema de Laplace?
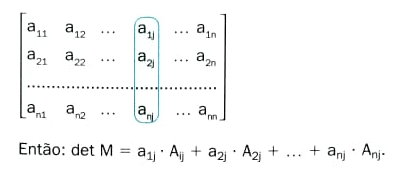
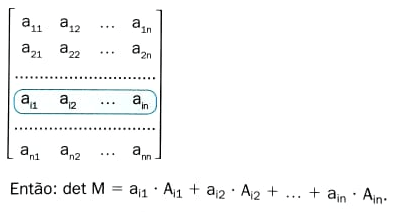
O determinante de uma matriz é a soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) pelos respectivos cofatores.
Para facilitar os cálculos, escolha a fila em que há uma maior quantidade de zeros. Em particular, se uma matriz tiver uma fila de zeros, seu determinante será zero.
Isto é:
a) Se escolhermos a coluna j da matriz M
b) Se escolhermos a linha i da matriz M
Observe o exemplo abaixo:
- Calcule o determinante da matriz M:
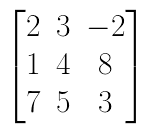
Como essa matriz tem ordem n ≥ 3, é conveniente usar o Teorema de Laplace.
Primeiramente, devemos escolher a fila (linha ou coluna) que tiver a maior quantidade de zeros, para facilitar os cálculos. Observando a matriz, verifica-se que ela não possui nenhum zero. Podemos então escolher qualquer linha ou coluna.
Escolhendo a primeira linha, para encontrar o determinante dessa matriz, iremos multiplicar cada um dos 3 elementos da primeira linha pelo seu respectivo cofator. Depois, somaremos os valores obtidos: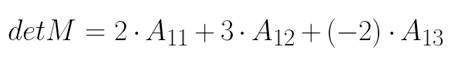 Vamos calcular agora os cofatores A11, A12 e A13:
Vamos calcular agora os cofatores A11, A12 e A13:

O determinante será:
det M = 2 . (-28) + 3 . 53 + (-2) . (-23)
det M = -56 + 159 + 46
det M = 149
Exercícios resolvidos
1) Dada a matriz M
Calcule o seu determinante usando o Teorema de Laplace.
RESOLUÇÃO
Primeiramente, devemos escolher uma linha ou coluna que possua o maior número de zeros. Nesse caso, a coluna 1 possui três números 0, enquanto a coluna 3 possui apenas um número zero. Iremos então escolher a coluna 1 para o cálculo do determinante.
Det M = 3 . A11 + 0 . A21 + 0 . A31 + 0 . A41
Det M = 3 . A11
Vamos agora calcular o cofator A11, que é dado por:
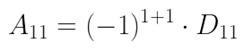
Para isso, precisamos calcular o menor complementar D11 do elemento a11 = 3. Suprima a linha 1 e a coluna 1. Em seguida, calcule o determinante da matriz que restou.
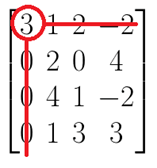
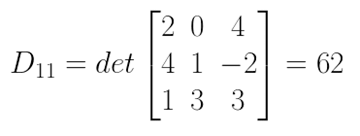
Em seguida, multiplique o resultado do menor complementar por (-1)i+j = (-1)1+1 = (-1)², encontrando finalmente o cofator A11.
![]()
Assim, o determinante será:
Det = 3 . A11 = 3 . 62 = 186.
Resumindo, o determinante foi calculado da seguinte maneira: