Teorema de Tales – O que é? Exercícios Resolvidos
A matemática é a repleta de Teoremas. Um teorema é uma espécie de afirmação provada como verdadeira, entrando, assim, para os livros de Matemática.
Um dos teoremas mais populares estudados no Ensino Médio, além do Teorema de Pitágoras, é aquele que denominamos por Teorema de Tales, também conhecido como Teorema das Linhas Proporcionais ou Teorema da Proporcionalidade de Segmentos.
Esse Teorema leva o nome do matemático grego Tales de Mileto, que viveu no século VI antes de cristo. Nessa época, a Geometria era amplamente utilizada. Por exemplo, os agrimensores usavam-na para medir terrenos, enquanto os comerciantes recorriam a ela para fazer edificações.
As famosas pirâmides, construídas próximas ao rio Nilo, no Egito Antigo, são um ótimo exemplo desse fato. Além da Matemática, Tales também deu contribuições relevantes tanto na Filosofia como na Astronomia, sendo considerando um dos sete sábios da Antiguidade.

Desafio da pirâmide Quéops
Hás muitas histórias sobre os feitos de Tales. Por exemplo, desafiado pelos escribas de um faraó, durante sua passagem pelo Egito Antigo, Tales determinou a altura da pirâmide Quéops, com a ajuda da luz do Sol, como ilustrado na figura.
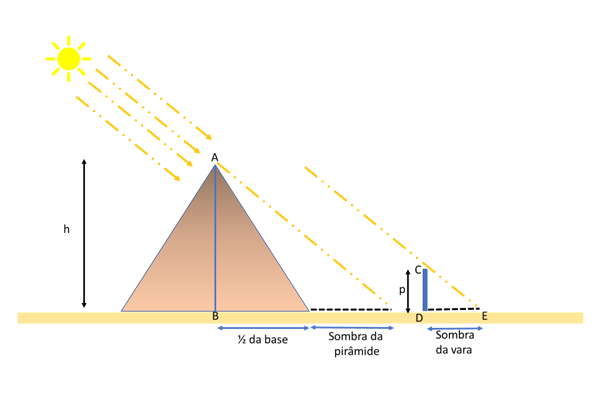
Percebeu, então, que, no momento em que a projeção da sombra do bastão de madeira adquiriu tamanho igual ao seu comprimento, por semelhança, a altura da pirâmide também seria igual ao comprimento de sua sombra.
Tales sabia que era preciso adicionar ao comprimento da sombra da pirâmide a metade do comprimento da sua base.
O que é o Teorema de Tales?
O Teorema de Tales será apresentado considerando a figura ao lado. Essa é desenhada a partir de cinco retas, formando vários segmentos, tais como AB, BC, MN, NP.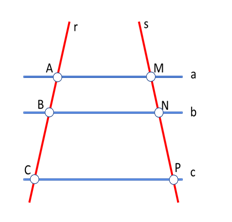
Antes de mais nada, duas retas são paralelas quando são equidistantes durante toda a sua extensão, portanto, não se interceptam em nenhum ponto.
Além disso, uma reta é transversal à outra se ambas apresentam apenas um ponto em comum. Portanto, as retas a, b e c são paralelas, enquanto as retas r e s são transversais.
O Teorema de Tales dita que: um feixe de paralelas determina em duas transversais segmentos que são proporcionais.
De acordo essa afirmação, podemos escrever a seguinte relação matemática entre os segmentos:
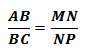
É correto afirmar que o segmento AB está para o segmento BC assim como o segmento MN está para o segmento NP. Ademais, podemos ainda considerar outras proporções, tais como:
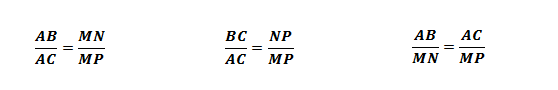
Exercícios resolvidos do Teorema de Tales
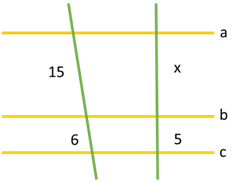
1- Na figura, temos a // b // c. Nessas condições, determine a medida indicada.
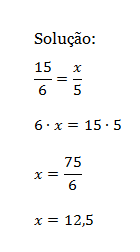
Teorema de Tales e os Triângulos
O Teorema de Tales pode ser aplicado nos triângulos quando traçamos uma reta paralela a um dos lados do triângulo, como mostra a figura ao lado – nesse caso, ao lado BC.
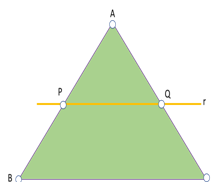
De acordo com o Teorema de Tales, pode-se escrever que:
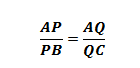
Portanto, temos: toda paralela a um lado de um triângulo, que encontra os outros dois lados em pontos distintos, determina, sobre esses dois lados, segmentos que são proporcionais.
[VEJA TAMBÉM: TRIÂNGULO RETÂNGULO – O QUE É?]
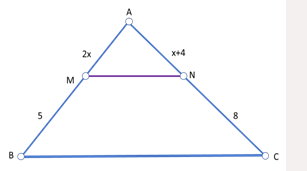
2- No triângulo ABC da figura abaixo, tem-se DE / / BC . Calcule as medidas dos lados AB e AC do triângulo.
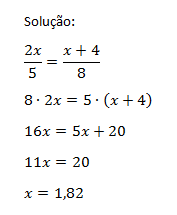
Teorema da bissetriz interna de um triângulo
 Outra relevante de aplicação do Teorema de Tales é o Teorema da bissetriz interna de um triângulo.
Outra relevante de aplicação do Teorema de Tales é o Teorema da bissetriz interna de um triângulo.
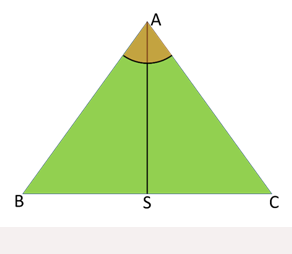
A bissetriz é uma semirreta que divide um ângulo ao meio, isto é, em dois ângulos congruentes, como mostra a figura do triângulo ABC ao lado.
A bissetriz interna do ângulo  determina sobre o segmento BC um ponto S. Para esse ângulo, os segmentos AB e AC são chamados de lados adjacentes, enquanto que os novos segmentos BS e SC são de lados opostos.
Portanto, a bissetriz de um ângulo interno de um triângulo determina, sobre o lado oposto, segmentos que são proporcionais aos lados adjacentes
Assim, se AS é a bissetriz do ângulo Â, então, de acordo com a afirmação destacada acima, podemos escrever a seguinte relação matemática:
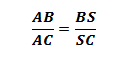
É correto dizer que o segmento AB está para o segmento AC assim como o segmento BS está para o segmento SC.
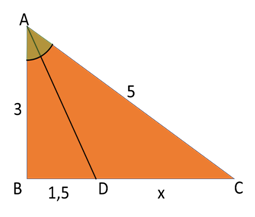
3- Na figura, o segmento AD é a bissetriz do ângulo Â. Determine a medida x indicada.
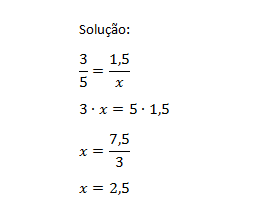





Deixe seu comentário