Considere um gás ideal: várias partículas que se comportam como bolinhas que se chocam sem perder energia dentro de um recipiente de um certo volume.
De acordo com a teoria cinética dos gases, a temperatura de um gás é proporcional à energia cinética média das partículas, ou seja, quanto mais rápidas e agitadas, maior a temperatura.
Além disso, quando se chocam nas paredes do recipiente, irão exercer uma força que na área interna do recipiente converte-se numa pressão. Se aumentarmos a temperatura então a pressão aumenta também.
Agora, se o volume aumenta, então as partículas possuirão mais espaço para se chocar e a pressão, por exemplo, será menor. Desta forma, como relacionar essas grandezas de pressão p, volume V e temperatura T quando há uma variação deles? Utilizamos a Equação Geral dos Gases Ideais abaixo:
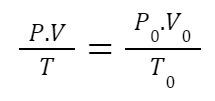
Ou seja, pode-se variar as grandezas, ocorrendo uma transformação de um estado inicial -parâmetros com o índice 0 (P0, V0, T0) – para um estado final – parâmetros sem o índice (P, V, T). Costumamos chamar a equação acima de “piviti povotó”.
Lei de Charles
Se a transformação ocorrer sem a mudança de uma das grandezas, utilizamos o prefixo iso: igual.
Transformação isobárica – sem variação de pressão.
Quando isso ocorre, podemos “cortar” a pressão, dividindo os dois lados por P. Assim, temos a Lei de Charles:
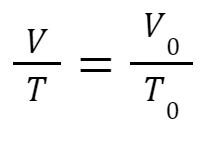
Ou seja, podemos entender que o quociente V0 por T0 nos fornece um valor constante. Se ocorrer um aumento de V, por exemplo, então T precisa aumentar também: um aumento de volume leva a um aumento de temperatura, e vice-versa. Dessa forma, numa transformação isobárica, as grandezas volume e temperatura serão diretamente proporcionais: se uma aumentar outra aumenta também.
Um gráfico de P por V fornece uma reta horizontal, pois a pressão é constante. Alguns problemas de transformação isobárica utilizam da interpretação deste gráfico para calcular o parâmetro desejado.
Referência
TIPLER, Paul A.; MOSCA, Gene. Physics for scientists and engineers. Macmillan, 2007.

