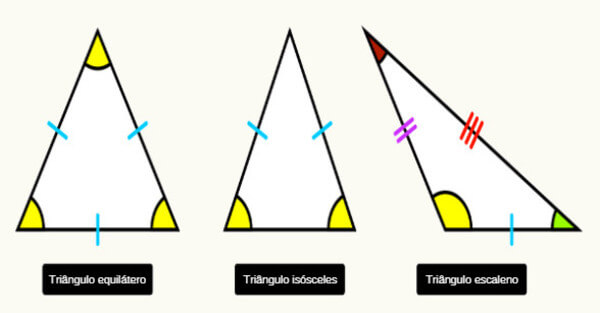
A geometria é o estudo da matemática que analisa o espaço que determinado objeto pode ocupar. O triângulo é uma das formas geométricas estudadas, principalmente em construções. Ele representa um polígono com o menor número de lados, podendo ser classificado de acordo com a medida dos seus lados, sendo: escaleno, equilátero ou isósceles.
O triângulo escaleno é aquele cujos 3 lados possuem medidas diferentes, no entanto a soma dos ângulos resulta 180º.
O que é o triângulo escaleno?
É um tipo de triângulo cujas medidas de todos os lados são diferentes, ou seja, são polígonos que não possuem um eixo de simetria.
Esse tipo é diferente dos triângulos equilátero e isósceles. O primeiro possui os 3 lados com a mesma medida, e o segundo conta com dois lados iguais e um diferente. O mesmo acontece com os ângulos internos, que podem ser classificados como triângulo acutângulo, retângulo e obtusângulo.
Exemplos de triângulo escaleno
Imagine um triângulo que possua um lado medindo 42cm, outro 52cm e o terceiro medindo 61cm. Esse é um triângulo escaleno, já que possui 3 medidas diferentes. No entanto, se possuísse dois lados com 43cm e um com 65cm seria um triângulo isósceles. Mas, se todos medissem 42cm seria um triângulo equilátero.
Com os ângulos, a regra é a mesma. Se um triângulo possui 3 ângulos diferentes, por exemplo, 67º, 42º e 71º, também é considerado escaleno. A soma de todos os ângulos deve ser de 180º.
Qual a área de um triângulo escaleno?
A área é o espaço que fica dentro do perímetro. Por exemplo, as paredes de uma casa formam um cômodo. O espaço interno entre essas paredes é chamado de área. Essa região é medida em m² ou cm². Para áreas muito extensas (como fazendas), usa-se como medida o acre, alqueire, hectare, centiare ou are.
Para calcular a área do triângulo escaleno, utiliza-se os conhecimentos da trigonometria.
A fórmula básica consiste em multiplicar a base (b) pela altura (h) e dividi-la por 2. Ou seja:
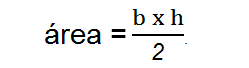
Caso todos os lados do triângulo sejam conhecidos, é possível calcular a área usando a seguinte fórmula de Heron:
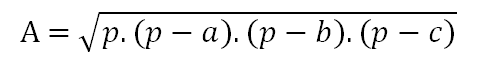
As medidas de “a”, “b”, e “c” correspondem à medida de cada lado do triângulo escaleno. E “p”, chamado de semiperímetro, pode ser obtido com a seguinte fórmula:
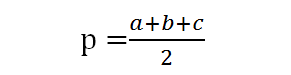
Já quando se conhece apenas a medida de 2 lados do triângulo escaleno e a medida do ângulo, usa-se a seguinte fórmula:
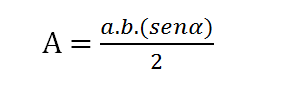
Como calcular o perímetro do triângulo escaleno
O perímetro é aquilo que delimita uma área. Por exemplo, as paredes de um quarto são o perímetro dele. Em resumo, significa o contorno de determinada área. A unidade de medida usada é m, cm ou km.
No entanto, é importante frisar que só é usado em figuras planas ou bidimensionais. Em figuras tridimensionais, como um cubo, calcula-se o volume.
Calcular o perímetro de um triângulo é bem simples, afinal, compreende a soma de todos os lados. Essa regra é válida para calcular o perímetro de qualquer forma geométrica.
A fórmula utilizada para o cálculo é:
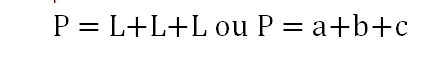
“P” representa o perímetro e “L” cada lado do triângulo. As letras “a”, “b” e “c” também representam cada lado do triângulo.
Exercícios resolvidos
Veja alguns exercícios resolvidos sobre como calcular a área do triângulo escaleno:
1- Calcule a área e o perímetro de um triângulo cujos lados medem 5cm, 7cm e 8cm.
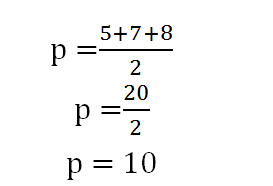
Sabendo a medida de todos os lados e de “p”, basta substituir na fórmula de área.
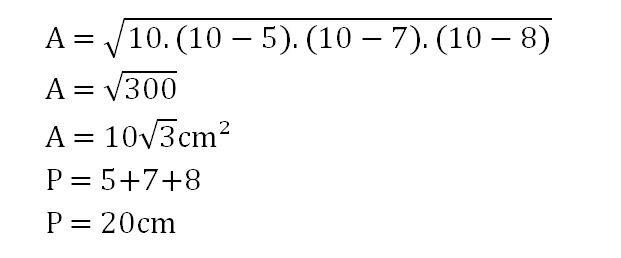
A área desse triângulo mede A = 10cm² e seu perímetro mede 20cm.
2- Calcule a área de um triângulo com as seguintes medidas: 8cm, 10cm e ângulo de 82.2º.
Primeiramente, é necessário calcular o seno de ângulo. Neste caso, o seno é igual a 0,992. Ao aplicar na fórmula, o cálculo é o seguinte:
A = 8.10.(0,992)/2
A = 80.0,496
A = 39,68
