O triângulo retângulo é uma forma geométrica, constituída de três cantos, um ângulo reto de 90° e outros dois cantos com ângulos menores que 90°.
O estudo das medidas do triângulo retângulo faze parte da trigonometria, ciência responsável por estabelecer relações entre formas geométricas planas.
Definição do triângulo retângulo
Cada parte do triângulo retângulo recebe nomes próprios da matemática, que facilitam na hora de encontrar suas grandezas ou aplicar fórmulas para calcular área e medidas. As denominações são:
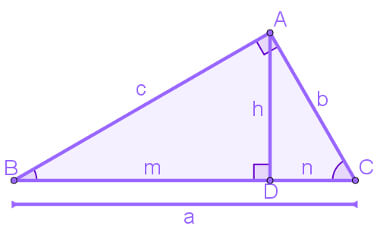
- Cateto oposto: é aquele que está no lado oposto ao ângulo principal;
- Cateto adjacente: é aquele que encosta no ângulo reto;
- Hipotenusa: é o lado oposto, sendo o maior lado do triângulo.
Já falamos sobre isso na explicação sobre seno, cosseno e tangente.
As 5 relações métricas do triângulo retângulo
As relações métricas do triângulo retângulo são as fórmulas que ajudam no cálculo das medidas dessa figura geométrica e, principalmente, para estabelecer a semelhança entre dois triângulos.
Para ilustrar a situação, o triângulo da imagem abaixo foi dividido em dois, sendo ACD e ADB. Com isso, podemos concluir algumas relações métricas:
1 – Hipotenusa do triângulo retângulo é igual à soma dos catetos sobre a hipotenusa. Tal afirmação resume-se na fórmula:
a = m + n
2 – O quadrado da hipotenusa é igual ao resultado dos catetos sobre a hipotenusa, ou seja:
h2 = m·n
3 – As medidas dos catetos são iguais ao quadrado da medida da hipotenusa. Essa fórmula matemática é chamada de Teorema do Pitágoras:
a² = b² + c²
Veja como calcular o teorema de Pitágoras, com exercícios resolvidos.
4 – A medida de um cateto pode ser calculada por meio da projeção sobre a hipotenusa. Isso quer dizer que:
c2 = an e b2 = an
5 – O resultado entre a divisão da hipotenusa e a altura de um triângulo retângulo é igual ao resultado da multiplicação de seus catetos. Tal raciocínio pode ser resumido em:
ah = bc
Relações trigonométricas do triângulo retângulo
As relações trigonométricas dessa forma geométrica são, na verdade, fórmulas que ajudam a calcular os ângulos internos e externos do triângulo retângulo. São elas:
Lei do Seno
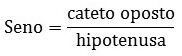
Determina que o seno é igual à divisão entre o cateto oposto e a hipotenusa.
Lei do Cosseno
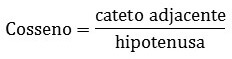
Determina que o cosseno é igual à divisão do cateto adjacente e da hipotenusa.
Lei da Tangente
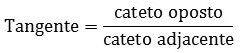
Determina que a tangente é o resultado da divisão entre o cateto oposto e o cateto adjacente.
Como calcular a área de um triângulo retângulo
Para calcular a área de um triângulo retângulo, é preciso calcular a metade da medida de um lado pela altura dividida por dois. O resultado é a quantidade de área que aquela forma possui.
Sendo assim, usa-se a fórmula:
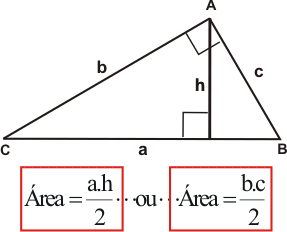
Exercício resolvido passo a passo
Para entender como aplicar a fórmula, confira a resolução da questão, abaixo:
(FUVEST) Uma escada de 10 metros está apoiada na parede de um prédio, formando um triângulo retângulo com as proporções de 8 e 6cm. Qual é a área formada entre escada e parede?
Primeiro, tentaremos identificar qual é a altura do triângulo. Por isso, aplicamos as grandezas já existentes na fórmula:
a·h = b·c
10·h = 8·6
10·h = 48
h = 48
10
Sabemos que a medida da altura é de 4,8cm. Agora, iremos aplicar a fórmula da área do triângulo retângulo.
A = 10·4,8
2
A = 48
2
O resultado da área é de 24 cm².

